6.4  The Black-Scholes Option Pricing Model

Here we use the riskless hedge approach to determine option prices.  The formal details of this approach are provided in Appendix D, topic D.4,  Derivation of the Black-Scholes Partial Differential Equation (PDE).

In the riskless hedge approach, you may recall from the binomial model that we have to construct a portfolio that is risk-free in every period.  Here, "every period" means continuously, since time evolves continuously.

We will show you here the option pricing solution, and then compare it to the option pricing model obtained in a world of certainty.  This comparison provides some interesting insight into the nature of the pricing model.

The Black-Scholes Analysis

Black and Scholes assume a model for stock price dynamics that is formally described as geometric Brownian motion and has the form:

Graphically, this describes a process that wanders around as depicted in Figure 6.5.

Figure 6.5

Stock Price as a Function of Time

In their seminal contribution to the theory of option pricing, Black and Scholes solve the option pricing problem for an option defined on a stock whose price follows such a process.  They assume that observed stock price movements resemble the behavior described by the Brownian motion in Figure 6.5.  From this assumption they derive the implied price process for a European option defined on the stock.

Since both the stock and the option prices share a common source of uncertainty, this derivation permits a riskless hedged portfolio to be constructed from the stock and its underlying option.  That is, this portfolio eliminates the common source of uncertainty for "an instant."  As a result, this portfolio in the absence of an arbitrage opportunity, will earn the instantaneous risk-free rate.

By creating this (instantaneously) riskless portfolio, Black and Scholes now have a portfolio that contains an observed stock price, plus an unobserved option price that equals a known risk-free rate.  By equating the instantaneous return from this hedged portfolio to the instantaneous risk-free rate, Black and Scholes are able to derive and solve an equation (often referred to as the Black-Scholes partial differential equation) for the price of a European option.

This price is important because a trader in a perfect market can rebalance the hedged portfolio continuously over the remaining life of the option.  That is, the riskless hedged portfolio is maintained over time, and in the absence of an arbitrage this portfolio will earn the continuously compounded risk-free rate. Therefore, the price obtained by Black and Scholes from this riskless hedged portfolio is the arbitrage free value of a European call option.  It should be noted that r in this model refers to the continuously compounded risk free rate of interest.  This is the rate of interest earned by the synthetic riskless hedge that is maintained over the life of the option.

The Black-Scholes Option Pricing Model

The call option price is:

where

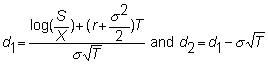
and N( ) is the cumulative standard normal distribution.  Thus, N(d1) is the probability that a normally distributed variable with mean 0 and variance 1 is less than d1.

Given the value of a European call option, the price of a put option follows from the put call parity relationship (see Chapter 2, topic 2.9), that must hold for European options in the absence of arbitrage.  Applying this relationship, the Black-Scholes price for a European put option is:

Example

The current price of a stock is $50.  Consider a (European) call option with one year to maturity and with a strike price of $50.  The volatility is estimated at 25% per annum, and the one-year continuously compounded interest rate is 10%.  What is the value of the call option?

Here,

            S = 50

            X = 50

            s = 0.25

            r = 0.1

            T = 1

Using the Option Calculator, you can verify that the call is worth $7.4879.

The value of a put option with the same parameters is $2.7298.

It is useful to compare the form of these pricing models with the option pricing model under certainty.

Comparison with Certainty Analysis

In the certainty model, for a call option we obtained

and the Black-Scholes price is

An important implication of this valuation model is that the value of the option is independent of the expected return from the underlying stock.  Equivalently, it is possible to value the option without knowing the true probability distribution of the stock.

We can now return to the IBM options discussed earlier in the certainty model.  Recall that the stock price less the present value of the dividend is $44.26, and the risk-free interest rate is 2.867%.  The options information was

The date of the information was Oct 15 1993, and the maturity date of the options was November 20, 1993.

To value these options using the Black-Scholes formula, we have

            S = 44.26

            r  = .02867

            T =  0.0986

The value of T is calculated by tallying the number of days to maturity and dividing by 365.

The strike price, X, ranges from 35 to 50.  In order to use the Black-Scholes formula, we need an estimate of volatility.  The historical volatility of the return of IBM had traditionally been estimated at 30% (i.e., s = 0.3).  This is calculated as follows.  Let rt = return from IBM stock between period t -1 and t:

Then, s is the standard deviation of the historical returns:

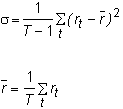
Typically, the standard deviation of returns is calculated on a monthly or weekly basis; this return is then annualized to get a number such as 30%. 

For the options at hand, we calculated the values of the options using three estimates of s : 30%, 35%, and 40%.  This leads to the following Black-Scholes prices for the call options, as compared to the actual bids and asks in the market on October 15, 1993.

For convenience, we have converted the quoted bids and asks into decimals.  As you can see, if s = 0.35, then the Black-Scholes model yields prices within the bid-ask spread, while option values obtained from the historical figure are slightly lower than the market prices.

Risk-Neutral Valuation Revisited

When we can construct the riskless hedge, and arbitrage arguments alone are sufficient to value derivative securities, we once again obtain the risk-neutral valuation principle (see Chapter 2, topic 2.7). Since risk attitudes do not matter, the option has the same value as in a hypothetical world where all investors are risk-neutral. 

In this risk-neutral world, the value of the option is the expected future value discounted by the continuously compounded risk-free rate.  Before taking the expectation and discounting it, note that the stock price must also equal the expected future value discounted by the risk-free interest rate.  But if the real world has risk-averse investors, this cannot be the case. You can see the problem as follows.

Let r  be the risk-free interest rate, and suppose that the risk adjusted discount rate in the real world is r:

S = E(ST)e-rT

The stock price in the real world is the future expected value discounted by r.  If investors are risk-averse, then we expect r>r (the difference between r and r  is called the risk premium).

In a risk-neutral economy, we discount E(ST) by r, and this value cannot  possibly equal S since r > r. 

The problem is that the expected cash flows are too high to be discounted by r.  To get the same stock price in the risk-neutral world, we must reduce the expected future cash flows.  This is done by changing the probability distribution from the true distribution to what is called the risk-neutral probability distribution.  You came across these probabilities in Chapter 2, topic  2.7, Risk-Neutral Valuation Principle. 

Once we have the risk-neutral probability distribution, we can think of our two worlds moving through time in a parallel fashion.  The first world is the real world.  The second world is the risk-neutral world, where the distribution of stock prices has been altered so as to be consistent with risk-neutrality. We know the price of the option in the risk-neutral world.  It is the expected future value discounted by the risk-free rate; the expectation is taken with the risk-neutral probability distribution.  Risk-neutral valuation tells us that this is also the price of the option in the real world.

The trick is to identify these "risk-neutral probabilities."  The Black-Scholes pricing model, however, yields these probabilities in the form of N(d1) and N(d2).  As a result, the value of the call option equals the stock price weighted by the risk-neutral probability minus the present value of the strike price weighted by another risk-neutral probability.  This interpretation of N(d1) and N(d2) as risk-neutral probabilities is provided in Chapter 5, topic 5.2, Binomial Option Pricing: N-Periods, because the Black-Scholes solution is exactly what we obtained in Appendix C  Chapter 5 Technical Topic:  Limiting Results.

In the next topic Interpretation of the Black-Scholes Model, we summarize some of the important implications of the Black-Scholes model and the methodology used to determine option prices.  In Chapter 13, topic 13.2, Applications: Stock Options, you will be introduced to using the online calculator  to determine the prices of commonly traded stock options.  You may want to immediately apply the option pricing model (using the calculator) to the stock data provided.

previous topic

next topic

(C) Copyright 1999, OS Financial Trading System