previous topic

6.5 Interpretation of the Black-Scholes Model

At first glance, the Black-Scholes formula for the value of a call option seems complex:

where

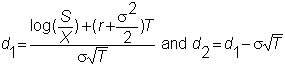
and N() is the cumulative standard normal distribution.

You can see that the option's value depends on five variables: the stock price, the risk-free interest rate, the stock's volatility, the strike price, and time. In Chapter 7, Hedge Parameters and Comparative Statics, we discuss how the option price varies with these parameters. Online, you can get an understanding of this dependence in Option Tutor's Option Sensitivities subject. If you are in this subject online select the option price for the Y-axis, and then systematically select the five variables for the X-axis.

Notice that the option price does not depend on the expected return from the option (or from the stock). In a conventional asset pricing model such as CAPM, you may recall that typically we value risky assets by discounting future cash flows by a risk-adjusted discount rate. The appropriate discount rate depends on risk attitudes of investors. These attitudes determine the "market price of risk," which is the rate at which you can trade risk for return.

In the Black-Scholes model, however, these considerations play no role. The reason has to do with the riskless hedge argument. In constructing the riskless hedge, what you are doing is diversifying all the risk from the option using the stock. In a precise sense, then, the option does not introduce any additional risk that must be priced in the market. Similarly, the option does not permit any additional risk to be diversified away by investors. Instead options permit a transfer of risk from buyer to seller.

Another way to see this is to return to the binomial model, where we use the stock and the bond to create a synthetic option. That argument shows you that the option is a redundant security, and therefore determining its price cannot involve any additional considerations of risk. All the risk that must be priced has already been accounted for in the stock price. From this approach you can also see that the option contract allows the transfer of but not the reduction of risk. In addition, because you can create a synthetic option from a stock and a bond, and the prices of these securities are observable, it should be clear that in principle the option value can be determined using these prices and arbitrage arguments.

Of course, these arguments all depend on knowing how to construct the riskless hedge. Both the binomial and geometric Brownian motion assumptions allow us to construct the riskless hedge. This would not be the case, for example, if the stock followed a trinomial process (as you saw in Chapter 4, topic 4.2's discussion of The Economics of Retrading). In that case, the option value cannot be determined by arbitrage arguments alone, and risk attitudes would again enter the picture.

An immense advantage of the Black-Scholes model is that it provides a closed-form solution for the option price. This means that, given the parameters required by the model, we can solve for the option value almost instantaneously. Chapter 13 lets you work through an application of this model to a real world option valuation problem.

The model also tells us how sensitive the option price is to the parameters. This is useful in managing the risk of an option position, which is the subject of Chapter 7, Hedge Parameters and Comparative Statics.

previous topic

next topic