![]() D.6 Derivation
of Stock Price Distribution
D.6 Derivation
of Stock Price Distribution
Let
the assumed process for stock prices be described by:
![]() .
.
The
solution to this stochastic differential equation is given by
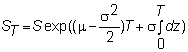
which
implies that

Since
dz is normally distributed with mean 0 and variance 1, we get
![]()
![]()
The
solution for ST
can be verified by applying Ito's lemma to log(S).
If
f(S,t) = log(S), then
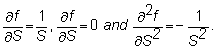
Since dS = mSdt + sSdz,
Ito's lemma yields
![]()
so
![]()
Thus,
log(S) is also a diffusion process, with drift
(m-s2/2) and volatility
s.
Integrating
from 0 to T yields

This
means that the change in log(S) between time 0 and time T, log(ST)-log(S),
is given by
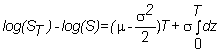
so

This
completes our characterization of the distributional properties implied from the
geometric Brownian motion model for stock prices.
(C) Copyright 1999, OS
Financial Trading System