13.2  Applications:  Stock Options

In this topic we apply the tools of option pricing theory to value options trading on IBM at the close of trading on March 24, 1994.  These are American options trading on (dividend-paying) IBM stock, traded on the Chicago Board of Trade (CBOT).

An American option on a dividend-paying stock immediately creates some practical problems.  The most formidable is that there is no closed-form solution to this type of valuation problem.  As a result, we have to resort to numerical methods to compute the option's value.

Online, you can apply the Option Calculator in Option Tutor to compute the values of (American) options traded on IBM.  Table 13.1 shows how option prices are quoted in the financial press (e.g. in The Wall Street Journal).   Column information is interpreted as follows.

Column 1:  The company name, IBM, and the stock’s closing price (from the NYSE).

Column 2:  The strike or exercise price of the option.

Column 3:  The expiration date of the option.  Recall that stock options expire on the Saturday after the third Friday of the month listed.

Column 4:  An estimate of open interest for the call option.  That is, the number of option contracts outstanding for all exchanges for the previous trading day (one contract is for 100 stocks).   Note that this information is one-day old, but the price information is current.

Column 5:  The last traded price for the call option.

Column 6:  Same as column 4, except for the put option; an estimate of open interest for the put option.

Column 7:  The last traded price for the put option.

A blank entry in the table means that the option did not trade.

Table 13.1

Option Prices

The timing of dividend-related complications are summarized in the time lines shown in Figure 13.1.   This figure shows you the  critical event dates for the four expiration months listed in Table 13.1.

Figure 13.1

IBM Option Event Dates

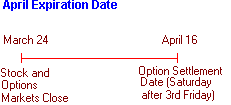
Critical Events

Markets have just completed trading on March 24, 1994.  This fixes the starting date for determining the remaining life of an option.

The options are settled on the Saturday after the third Friday of the expiration month. The expiration dates are shown on the time lines.

We have to convert the remaining life of each option into a proportion of a year.  For example, you can calculate that there are 58 days remaining in the life of any May expiration IBM option.  The option pricing model requires us to express the remaining life in days as an "annualized time," which here is 58/365 = 0.1589 of a year. 

Online, you can enter the May expiration date, 5/21/94, as well as “today's date” (which here is 3/24/94) into the date calculator.  If you click on OK, the date calculator will automatically place the value 0.1589 into the Maturity field of the calculator.

The remaining two events in the time line relate to dividends.  Observe that IBM stock goes ex-dividend twice during the lives of these options.  The first is in May, and this affects all but the April option.  The second is in September, which only affects the October option.  Dividends affect option values, because if you buy a stock after ex-dividend date, you do not get the dividends just declared (although you would be entitled to future dividends).

The effect of the May ex-dividend date is that IBM's stock price will adjust for the dividend on this date, (even though the actual payment date is June 6, 1994).   Since the value of the option depends on the stock price, the ex-dividend price is what is relevant to optionholders.  Similarly, the price will change when the stock goes ex-dividend in September.  The effects of these dividend payments need to be taken into account when valuing the option on March 24.

In order to apply the Black-Scholes option pricing model, we adjust the current IBM stock price by the present value of the projected dividend payment.  To do so we need to know five pieces of information:

1.  The contractual details of the option, such as maturity date, strike or exercise price, type (American or European), and whether it is a put or a call.

2.  The term structure of default-free interest rates.

3.  Estimated dividends over the life of the option.

4.  The volatility of IBM stock.

5.  The appropriate discount rate for critical cash flow events (such as the payment of dividends).

IBM options are American and the current strike prices being traded are provided in Table 13.1. The time to maturity is computed from the current date (now) to the Saturday after the third Friday of the option's expiration month.

For interest rates, we use the yields on Treasury bills that mature at dates very close to the option maturity date and also the ex-dividend date.  For the latter we will assume that the default-free interest rate is accurate to the cent.  These yields (on March 24) are shown in Table 13.2.

Table 13.2

Treasury Bill Yields 

This table gives you appropriate risk-free interest rates for the option valuation problem.  You may recall that in the Black-Scholes model, interest rates are assumed to be constant.  As the table reveals, in fact they vary with the time to maturity. 

To accommodate this problem, we simply make an approximation that is widely used in practice: we value the option using the yield to maturity of the Treasury bill closest to the maturity date.  For an appropriate discount rate for dividends, given the relatively short times involved, the term structure of Treasury bills provides a close enough estimate. 

IBM's last quarter dividend is our estimate for the current quarter's dividend.  Information on IBM's recent dividend history appears in Table 13.3.

Table 13.3

IBM’s Recent Dividend History 

The closing stock price of IBM on March 24, 1994, was $56.375.  For all but the April options, we have to subtract the present value of both dividend payments.  For the May option, we have to subtract only the present value of the first dividend.

When adjusted for the present value of one dividend payment, the "stock price"  equals $56.127.  When adjusted for the present value of both dividend payments, it equals $55.879.

Finally, we need to estimate the volatility.  The Black-Scholes model assumes that the volatility remains constant over time.  Suppose that volatility has been estimated from recent IBM activity to be 0.30, or 30%, on an annualized basis.  Later, you will see how volatility can be inferred from current option prices; this will let you compute your own estimates of volatility.  Volatility can also be estimated using the historical standard deviation of the stock return; in this case, the estimate is called the historical volatility.

We will value the options that are close to being "at-the-money."  Online, you can compute your own values using the calculator.  Observe that there are four maturity months:  April, May, July, and October.  Table 13.4 provides the relevant data for each maturity month for the Option Calculator.

Table 13.4

Maturity Month Data 

We consider here only the strike $55 options and leave additional pricing problems as  exercises.  You can observe that for April options there are no dividends, so this assumption of the basic model is met. 

Call Option

Since an American call option on a non-dividend-paying stock has the same value as a European call option, you can compute the April call values directly using the Black-Scholes formula.

The variables are:

The Black-Scholes price (binomial option price) is 2.52. The market price is 2.50.  An interesting check on these prices is to compute the American option value using the binomial (200 iterations).  Under these conditions, it should provide the same answer as the Black-Scholes value, which it does.  The finite difference approximation, however, is not as accurate for a grid size of 200 x 200  (Call price = 2.275).

Put Option

For an April put option, the European option price is not correct, because it may be worth exercising an American put early with or without dividends.  But you can see that the European formula still provides a reasonable approximation. As expected, however, the binomial model value for the American put option is a little higher than the European price.

Black-Scholes put price:         1.029

Binomial American put price:  1.035

Market price:                           1.00

At the assumed volatility, both models slightly overprice the option relative to the actual market price. 

For other maturities you can use the dividend-adjusted prices for both the Black-Scholes (European pricing) model as well as the binomial pricing model.  For both types of American options, this adjustment is a little crude because it does not fully take into account the value of early exercise.  We suspect that this affects the put option's value more than the call option's value.

Online, you can use the calculator to verify the numbers in Table 13.5.

Table 13.5

Options Data 

You can observe that the constant volatility, dividend-adjusted model provides a fairly accurate estimate of the market values for the call options.  The longer-maturity call options are within one cent, and only the May maturity varies by more than three cents.

The American put option is less accurate, which is not surprising, because we are using the present value of the dividend adjustment, which understates the value of early exercise.  Later we will see another proxy for dividend adjustment, called the constant dividend yield model, and we will examine the result of this adjustment.

Implied Volatilities and Informational Implications from Option Prices

Given option prices, we can turn the option pricing problem around to ask the question:  What is the implied volatility?

What this means is that we take the pricing model as being fixed, and find the volatility that makes the model price equal to the market price.  This estimate of volatility is called the implied volatility.

When we do this, you will see that the constant volatility assumption may be inappropriate.  Table 13.6 provides the implied volatilities for both the Black-Scholes and the binomial pricing models (using 50 steps) for the May-maturity options.

Table 13.6

Implied Volatility Estimates 

You can see evidence of what is called the "volatility smile" developing in the put options, although not in the call options.  The volatility smile is a systematic pattern of implied volatilities that are high for low strike prices, then fall as strikes increase, but increase again as strike prices increase further.  This pattern traces out the shape of a smile when graphed, which gives rise to its name.

Different implied volatility shapes are often taken as evidence of stochastic volatility.  If volatility is indeed stochastic, then the option pricing models discussed so far are missing a risk premium term.  This term compensates risk-averse investors for this source of risk. 

In our case, the May 65 call option appears to be underpriced relative to the other call options, yet the May 60 put appears to be overpriced relative to the other puts.  This type of observation is consistent with a stock price distribution that deviates from the lognormal distribution.  In particular, these prices are consistent with a market distribution that has a fatter left tail than is assumed by the pricing model.  That is, prices are consistent with a market that is putting more weight on the possibility of an IBM price decline on March 24, 1994, than would be the case with a lognormal distribution.

If this is the case, we would expect to get the smile in the put options.  We would expect no smile in the call options.

By the way, the price of IBM declined in the days following March 24!

In the next topic, Applications:  Currency Forwards and Futures, we will work through an application of the theory to the currency markets.

previous topic

next topic

(C) Copyright 1999, OS Financial Trading System