![]() 12.4 Application:
Currency Options
12.4 Application:
Currency Options
From
the Lemma the excess drift rate divided by the volatility is equal for the stock
and the call option. This means
that again we merely have to simplify the equation
![]()
The two assets are the
call option and SBd, the value of the deliverable bond in the strike currency.
The price of the call option is always in units of the strike currency
(k); the exchange rate is the number of units of the deliverable currency in
units of the strike currency.
The exchange rate
process is
![]()
The call option, C,
is assumed to be a function of S and t. Ito's lemma implies
that the drift rate of the call option is:
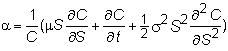
and
the volatility is
![]()
The second asset is SBd.
Bd
grows at rate rd
where d denotes units of
deliverable currency:
![]()
Totally
differentiating SBd,
we get d(SBd) = S(dBd) + (dS)Bd.
Substituting for dS and dBd,
we find that
![]()
The
general method for valuing options then implies that
![]()
If we
substitute for a
and q and simplify, we get the partial differential equation for the currency
call option:
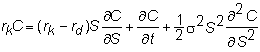
This equation differs
from the original Black-Scholes equation by only the continuous zero-coupon bond
yield. The continuous dividend yield PDE is reproduced for your convenience as:
![]()
You can see that the
solution to the currency option PDE must be the same as the continuous dividend
yield case when rd is substituted for the constant continuous dividend yield
term q, and rk
is substituted for r.
In the next topic, Application:
Options on Futures, we apply the same technique to derive Black's
Model for options on futures.
(C) Copyright 1999, OS
Financial Trading System